Intermediate Value Theorem

Source http://www.mathsisfun.com/algebra/intermediate-value-theorem.html

The idea behind the Intermediate Value Theorem is this:

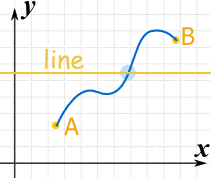When we have two points connected by a continuous curve: one point below the line the other point above the line ... then there will be at least one place where the continuous curve crosses the line!

Well of course we must cross the line to get from A to B!

Now that you know the idea, let's look more closely at the details.

Continuous

The curve must be continuous ... no gaps or jumps in it.

Continuous is a special term with an exact definition in calculus, but here we will use this simplified definition:

we can draw it without lifting our pen from the paper

More Formal

Here is that idea stated more formally:

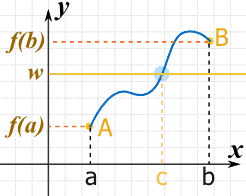		When: The curve is the function y = f(x), which is continuous on the interval [a, b], and w is a number between f(a) and f(b),
		Then ...

... there must be at least one value c within [a, b] such that f(c) = w

In other words the function y = f(x) at some point must be w = f(c)

Notice that:

• w is between f(a) and f(b), which leads to ...
• c must be between a and b

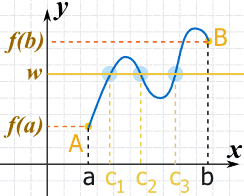
At Least One It also says "at least one value c", which means we could have more. Here, for example, are 3 points where f(x)=w.

How Is This Useful?

Whenever we can show that:

• there is a point above a line
• and a point below a line, and
• that the curve is continuous,

we can then safely say "yes, there is a value somewhere in between that is on the line".

Example: is there a solution to x⁵ - 2x³ - 2 = 0 between x=0 and x=2?

At x=0:

0⁵ - 2 × 0³ - 2 = -2

At x=2:

2⁵ - 2 × 2³ - 2 = 14

Now we know:

• at x=0, the curve is below zero
• at x=2, the curve is above zero

And, being a polynomial, the curve will be continuous,

so somewhere in between, the curve must cross through y=0

Yes, there is a solution to x⁵ - 2x³ - 2 = 0 in the interval [0, 2]

Question 1

Functions (Calculus, General)

Help

Between which of the following two values does the equation 3x³ + 5x - 11 = 0 

have a solution?

A

Between -2 and -1

B

Between -1 and 0

C

Between 0 and 1

D

Between 1 and 2

D is the correct answer

Let f(x) = 3x³ + 5x - 11
Therefore
f(-2) = 3 × (-2)³ + 5 × (-2) - 11 = -24 - 10 - 11 = -45 < 0
f(-1) = 3 × (-1)³ + 5 × (-1) - 11 = -3 - 5 - 11 = -19 < 0
f(0) = 3 × 0³ + 5 × 0 - 11 = 0 - 0 - 11 = -11 < 0
f(1) = 3 × 1³ + 5 × 1 - 11 = 3 + 5 - 11 = -3 < 0
f(2) = 3 × 2³ + 5 × 2 - 11 = 24 + 10 - 11 = 23 > 0

Since f(1) < 0 and f(2) > 0 and f is a polynomial, the Intermediate Value Theorem tells us that f(x) = 0 for some value of x between 1 and 2.

Question 3

Functions (Calculus, General)

Help

Between which of the following two values does the equation 

-7x³ + 20x² - x + 1 = 0 have a solution?

A

-1 and 0

B

0 and 1

C

1 and 2

D

2 and 3