A polynomial looks like this:
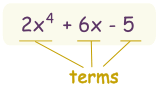 | ||||||||||||
example of a polynomialContinuous and Smooth
There are two main things about the graphs of Polynomials:
The graphs of polynomials are continuous, which is a special term with an exact definition in calculus, but here we will use this simplified definition:
 we can draw it without lifting our pen from the paper we can draw it without lifting our pen from the paper
The graphs of polynomials are also smooth. No sharp "corners" or "cusps"
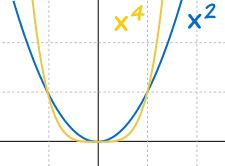
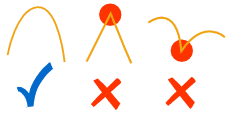 How the Curves Behave
Let us graph some polynomials to see what happens ...
... and let us start with the simplest form:
f(x) = xn
Which actually does interesting things:
And:
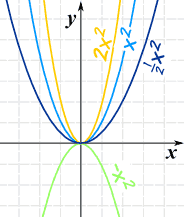
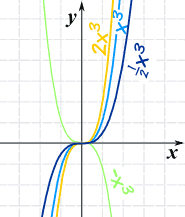
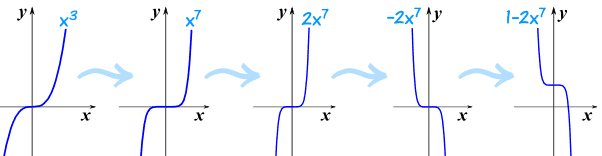
Power Function of Degree n
Next, by including a multiplier of a we get what is called a "Power Function":
f(x) = axn
f(x) equals a times x to the "power" (ie exponent) n
The "a" changes it this way:
We can use that knowledge when sketching some polynomials:
Turning Points
A Turning Point is an x-value where a local maximum or local minimum happens:
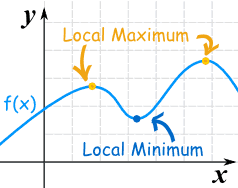 How many turning points does a polynomial have?
Never more than the Degree minus 1
The Degree of a Polynomial with one variable is the largest exponent of that variable.
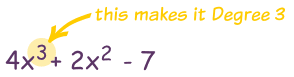
We may not know where they are, but at least we know the most there can be!
What Happens at the Ends
And when we move far from zero:
then the graph starts to resemble the graph of y = axn where axn is the term with the highest degree.
This is officially called the "End Behavior Model".
And yes, we have come to the end!
Summary
![[image]](https://www.mathopolis.com/questions/images/0/e/8e951727655dca3864ffb2d46b9b642.jpg) Which one of the following could be the function for the above graph?
A
f(x) = 3 - 2x5
B
f(x) = 3 - 2x6
C
f(x) = 3 + 2x6
D
f(x) = 3 - 2x2
|
The graph is upside down indicating that the power of x should be preceded by a negative. This means the answer could be B or D.
Since the curve is flattened at the top and does not show the characteristic shape of a parabola, we conclude that B is the correct answer.
Furthermore, the y-intercept is 3 which agrees with this answer.
![[image]](https://www.mathopolis.com/questions/images/4/c/dd94d138b44fb0a5610fed6f3e05272.jpg)
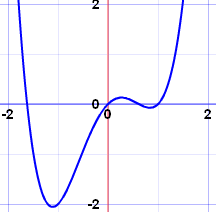
The above shows the graph of y = 2x5- 6x3
How many turning points does it have?
A
2
B
3
C
4
D
Cannot say
At a maximum turning point the slope of the curve changes from positive to zero to
negative - there is a maximum turning point at approximately (-1.4, 5.8).
At a minimum turning point the slope of the curve changes from negative to zero to
At a minimum turning point the slope of the curve changes from negative to zero to
positive - there is a minimum turning point at approximately (1.4, -5.8).
At the origin the slope of the curve changes from negative to zero and then back to
At the origin the slope of the curve changes from negative to zero and then back to
negative - this is called a point of inflection and is not a turning point.
Far away from the origin the graph of y = 2x5-6x3 behaves like the graph of y = 2x5,
Far away from the origin the graph of y = 2x5-6x3 behaves like the graph of y = 2x5,
so there will be no further turning points.
Therefore, there are just 2 turning points.
![[image]](https://www.mathopolis.com/questions/images/d/7/76fa4091499c3bf03eb7eede8489e12.jpg)
Which one of the following could be the function for the above graph?
Therefore, there are just 2 turning points.
![[image]](https://www.mathopolis.com/questions/images/d/7/76fa4091499c3bf03eb7eede8489e12.jpg)
Which one of the following could be the function for the above graph?
A
f(x) = 1 - 3x4
B
f(x) = 1 + 3x4
C
f(x) = (1 - 3x)4
D
f(x) = (1 + 3x)4
The graph is symmetrical about the y-axis, which means the function is even.
When expanded the answers C and D have both even and odd powers, so they are
neither even nor odd functions. So the answer cannot be C or D.
Which leaves only A or B.
The graph is upside down indicating that the power of x should be preceded by a negative.
Therefore the answer is A.
![[image]](https://www.mathopolis.com/questions/images/d/5/994f6c1e94c06ab48cdf26a22abcbd2.jpg)
Which one of the following could be the function for the above graph?
correct answer
![[image]](https://www.mathopolis.com/questions/images/2/2/562e63ef48954674c409a9e547ee412.gif)
Using the Function Grapher, my first attempt to the solution is that it has a minimum point somewhere between x = -1 and x = 0.
![[image]](https://www.mathopolis.com/questions/images/e/f/e8499e4672751fe7a4518c09b0a8f02.gif)
When I zoom in, I get a better approximation, which is the point (-0.6, -0.9) to 1 decimal place.
So the minimum value of the function is -0.9 correct to 1 decimal place.
(Note: the function could have been simplified to f(x) = 2x4 + 2x)
When expanded the answers C and D have both even and odd powers, so they are
neither even nor odd functions. So the answer cannot be C or D.
Which leaves only A or B.
The graph is upside down indicating that the power of x should be preceded by a negative.
Therefore the answer is A.
![[image]](https://www.mathopolis.com/questions/images/d/5/994f6c1e94c06ab48cdf26a22abcbd2.jpg)
Which one of the following could be the function for the above graph?
A
y = x6 - 5x4 + 7x2
B
y = x3 + 7x
C
y = x5 - 5x3 + 7x
D
y = x5 - 5x2 + 7x
The graph has point symmetry about the origin, which means the function is odd.
This rules out answer A which is even and answer D, which is neither even nor odd.
The graph has 4 turning points, so it cannot be a cubic - a cubic has at most 3 - 1 = 2
The graph has 4 turning points, so it cannot be a cubic - a cubic has at most 3 - 1 = 2
turning points. So answer B cannot be correct.
A quintic, on the other hand, has at most 5 - 1 = 4 turning points, so C could be the
A quintic, on the other hand, has at most 5 - 1 = 4 turning points, so C could be the
correct answer
Use the Function Grapher at http://www.mathsisfun.com/data/function-grapher.php to find an estimate, correct to 1 decimal place, of the minimum value of the function
f(x) = 5x4 - 3x4 + 2x
(Note: enter function as 5x^4-3x^4+2x ... or in a simpler form if you can think how.)
f(x) = 5x4 - 3x4 + 2x
(Note: enter function as 5x^4-3x^4+2x ... or in a simpler form if you can think how.)
A
-0.6
B
-0.8
C
-0.9
D
-1.9
![[image]](https://www.mathopolis.com/questions/images/2/2/562e63ef48954674c409a9e547ee412.gif)
Using the Function Grapher, my first attempt to the solution is that it has a minimum point somewhere between x = -1 and x = 0.
![[image]](https://www.mathopolis.com/questions/images/e/f/e8499e4672751fe7a4518c09b0a8f02.gif)
When I zoom in, I get a better approximation, which is the point (-0.6, -0.9) to 1 decimal place.
So the minimum value of the function is -0.9 correct to 1 decimal place.
(Note: the function could have been simplified to f(x) = 2x4 + 2x)

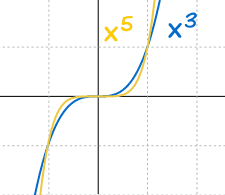

Không có nhận xét nào:
Đăng nhận xét