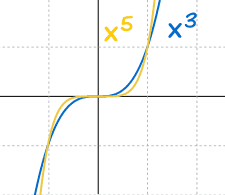https://tungnt31.wordpress.com/category/d%E1%BB%8Dc-d%E1%BB%83-suy-ng%E1%BA%ABm/
Thứ Năm, 23 tháng 6, 2016
LÀM THẾ NÀO ĐỂ TĂNG TỐC ĐỘ ĐỌC SÁCH MÀ KHÔNG CẦN HỌC KỸ THUẬT ĐỌC NHANH?
Đọc sách nhanh hơn - đó là mơ ước của nhiều bạn, trong đó có cả mình. Nhưng đọc sách nhanh thì có lợi ích gì, và làm thế nào để đọc sách nhanh hơn thì không phải ai cũng biết cách.
Có thể các bạn đã nghe tới những kỹ thuật đọc nhanh (kiểu như phương pháp đọc nhanh của Tony Buzan hay của nhiều người khác đã share trên mạng), bản thân mình cũng đã thử nhiều lần nhưng nhận ra rằng nó đòi hỏi sự tập trung rất cao và dễ khiến đa số mọi người cảm thấy không quen và nản chí ngay từ giai đoạn đầu.
Tuy nhiên có một số cách đơn giản (cả về mặt kỹ thuật lẫn tư duy) có thể giúp bạn đọc tăng tốc độ đọc hiểu của mình lên thì hiếm thấy ai nhắc tới. Vậy nên sau một thời gian kiểm chứng, hôm nay mình muốn chia sẻ tới các bạn những kinh nghiệm này của bản thân, hy vọng chúng sẽ hữu ích cho các bạn.
Đầu tiên, tự hỏi bản thân xem tại sao mình lại muốn đọc nhanh hơn, đọc nhanh hơn thì có lợi ích gì? Theo mình thì việc đọc sách nhanh sẽ mang lại cho bạn những lợi ích thiết thực sau:
1/ ĐỌC SÁCH NHANH HƠN GIÚP TIẾT KIỆM THỜI GIAN VÀ NỖ LỰC CỦA BẠN.
Tiết kiệm thời gian là điều tất nhiên, ai cũng biết rồi, vậy tại sao nó lại tiết kiệm nỗ lực cho bạn. Lấy 2 ví dụ đơn giản, bạn thử trả lời xem nhé:
VD1: Bạn làm một công việc có deadline và một công việc được làm trong thời gian không giới hạn. Theo bạn, loại công việc nào sẽ khiến cho bạn làm việc một cách tập trung, nghiêm túc và hoàn thành nó nhanh chóng hơn?
VD2: Bạn tham gia một cuộc đua xe đạp dài 20km và cũng vẫn độ dài ấy nhưng bạn lại đi xe đạp để du lịch. Theo bạn, trường hợp nào bạn sẽ hoàn thành chặng đường một cách nghiêm túc, tập trung và nhanh chóng hơn?
Câu trả lời cho cả 2 ví dụ tuyệt nhiên là phương án 1. Vậy tại sao chúng ta lại không liên hệ chúng với việc đọc sách. Đã bao nhiêu lần bạn đọc một cuốn sách và cảm giác như nó dài bất tận, và đã bao nhiêu lần bạn đọc dở một cuốn sách và không tiếp tục đọc lại nó nữa? Mình cá là rất nhiều lần, kể cả mình cũng vậy. Lý do rất đơn giản, bạn càng kéo dài thời gian đọc sách, bạn càng ít nỗ lực và tập trung hơn để hoàn thành nó, càng dành ra ít nỗ lực để hoàn thành nó, bạn càng cảm thấy mệt vì thời gian để làm việc đó bị kéo dài dường như vô tận. Vậy nên hãy cố hoàn thành việc đọc một cuốn sách (hay bất kỳ một việc gì khác) trong một thời gian hạn định, nó sẽ giúp bạn tiết kiệm được thời gian và sức lực rất nhiều.
2/ ĐỌC SÁCH NHANH HƠN GIÚP BẠN HẤP THỤ ĐƯỢC SÁCH CẢ VỀ SỐ LƯỢNG LẪN CHẤT LƯỢNG TỐT HƠN.
- Về số lượng: tất nhiên rồi, bạn càng mất ít thời gian hơn để hoàn thành một cuốn sách, bạn càng có nhiều thời gian hơn để đọc những nội dung khác. Quỹ thời gian thực là không đổi, nhưng thời gian để hoàn thành một cuốn sách là có thể thay đổi.
- Về chất lượng: nhiều người nghĩ rằng đọc sách nhanh thì sẽ bỏ qua mất nhiều nội dung của sách, hay bỏ qua luôn cả công đoạn ngẫm nghĩ sách và sẽ nhanh quên nên thà đọc chậm còn hơn. Đây là một lỗi tư duy thường gặp (và mình cũng đã từng gặp phải) nhưng xin thưa rằng nó không hoàn toàn đúng. Mình sẽ giải thích ở phần dưới cho các bạn. Nhưng xin khẳng định việc đọc sách nhanh hoàn toàn có thể giúp bạn đạt được mục đích thâu tóm được mặt chất lượng của cuốn sách - tức nội dung của nó - một cách hiệu quả.
--------------------------------------------------------------------
NHỮNG TƯ DUY VÀ PHƯƠNG PHÁP ĐỂ "NUỐT CHỬNG" MỘT CUỐN SÁCH NHANH HƠN.
1/ THẾ NÀO LÀ NHANH?
Đầu tiên, chúng ta phải định nghĩa được thế nào là NHANH. NHANH là một khái niệm tương đối, với người A thì nhanh phải là đọc 1 trang 1 phút, người B thì phải 2 trang 1 phút mới gọi là nhanh. Bởi vậy mà mình chỉ dùng từ NHANH HƠN chứ không dùng từ NHANH. Nhưng bạn yên tâm, cứ mỗi lần bạn NHANH HƠN một chút cũng là bạn đang đạt tới tốc độ NHANH mà bạn đặt ra cho mình.
2/ VẪN CÂU HỎI : THẾ NÀO LÀ NHANH?
Nhiều người nghĩ rằng đọc nhanh là phải đọc CON CHỮ nhanh, tức là trong một thời gian nhất định bạn phải ngấu nghiến được nhiều câu nhất, nhiều dòng nhất, nhiều trang nhất có thể. Nếu như hiểu rằng NHANH là vậy thì chúng ta đang bỏ quên mất thứ quan trọng nhất mà chúng ta cần khi đọc một cuốn sách, đó là THÔNG ĐIỆP.
Nhiều người nghĩ rằng đọc nhanh là phải đọc CON CHỮ nhanh, tức là trong một thời gian nhất định bạn phải ngấu nghiến được nhiều câu nhất, nhiều dòng nhất, nhiều trang nhất có thể. Nếu như hiểu rằng NHANH là vậy thì chúng ta đang bỏ quên mất thứ quan trọng nhất mà chúng ta cần khi đọc một cuốn sách, đó là THÔNG ĐIỆP.
Ví dụ thế này nhé, mình sẽ mô tả một cô gái:
"Có một cô gái rất xinh đẹp đang đứng ở bên chiếc máy bay của tổng thống Obama. Cô ta mặc một chiếc áo thun màu đen, ở giữa chiếc áo thun là một hình vẽ giống như một bông hoa nhưng với hoa văn rất cầu kỳ và kỳ lạ. Bông hoa ấy xanh nước biển, ở giữa là nhụy màu hồng và điểm những chấm nhỏ tựa như những con ong đang hút mật ở đó. Chiếc quần cô ta mặc cũng kỳ quái không kém, nó giống như một chiếc quần thổ cẩm nhưng làm bằng chất liệu như của quần jean. Một tay cô ta xỏ vào túi quần, tay kia cầm điếu xì gà Cu Ba. Cứ vài giây, cô ta lại đưa điếu xì gài lên miệng rít từng hơi một và nhả ra một làn khói trắng xóa bao phủ cả chiếc kính râm thời thượng của mình..."
Ok, bạn đọc xong rồi chứ. Vậy cho mình hỏi với một đoạn ngắn như vậy bạn nhớ được những gì về cô gái. Có thể sẽ chỉ là: "Một cô gái xinh đẹp đang đứng cạnh một chiếc máy bay" hoặc thứ đọng lại trong bạn là HÌNH ẢNH về một cô gái với những chi tiết như mình miêu tả.
Rõ ràng là trong đầu chúng ta không tua lại từng con chữ, mà nó tóm gọn lại bằng một Ý CHÍNH nào đó, hoặc bằng một HÌNH ẢNH cụ thể.
Tưởng tượng rằng khi bạn nói chuyện với mình, mình sẽ miêu tả lại cô gái trên cho bạn nhưng là bằng lời nói, tốc độ não bạn phải xử lý thông tin sẽ nhanh hơn rất rất nhiều so với khi bạn đọc. Và kết quả là bạn tóm gọn nó thành một Ý CHÍNH hay một HÌNH ẢNH, chứ bạn không tua lại từng câu, từng chữ mình nói. Mà bản chất của văn bản lại là một dạng lưu ÂM THANH bằng CHỮ VIẾT (giống như ghi âm vậy).
Vậy tại sao chúng ta chưa bao giờ nghi ngờ khả năng nắm bắt thông điệp của mình khi giao tiếp bằng lời nói nhưng lại luôn sợ rằng khi mình đọc nhanh thì sẽ bỏ qua mất thông điệp cuốn sách muốn truyền tải, mặc dù tốc độ bạn phải xử lý thông tin khi nghe nhanh hơn gấp nhiều lần tốc độ xử lý thông tin khi đọc. Quả là vô lý!
Vậy nên một lần nữa, chúng ta thấm thía rằng chúng ta đọc là để nắm bắt THÔNG ĐIỆP thay vì nắm bắt CON CHỮ.
3/ LÀM THẾ NÀO ĐỂ NẮM BẮT THÔNG ĐIỆP NHANH HƠN?
Ok, sau khi đã hiểu bản chất của đọc là nắm bắt THÔNG ĐIỆP thì câu hỏi tiếp theo được đặt ra là làm thế nào để nắm bắt THÔNG ĐIỆP nhanh hơn.
Chắc hẳn có rất nhiều bạn biết đến nguyên lý 80/20 của nhà kinh tế học người Ý Pareto. Nếu muốn tìm hiểu nguyên lý này các bạn có thể tìm đọc trên mạng, còn trong nội dung bài viết này thì mình sẽ tóm gọn ý nghĩa của nguyên lý này như sau:
20% CON CHỮ TRONG MỘT CUỐN SÁCH CHIẾM TỚI 80% KHỐI LƯỢNG THÔNG ĐIỆP SÁCH MUỐN TRUYỀN TẢI.
Con số 80/20 chỉ là tương đối mà thôi, nên có khi là 5% con chữ trong sách đã truyền tải tới 95% thông điệp sách muốn truyền tải rồi. À, các bạn đừng nhầm lẫn là X% + Y% cứ phải ra tổng 100% nhé, nó có thể ít hơn hoặc nhiều hơn. Nhưng mình không nói bạn sẽ hiểu được 100% sách muốn truyền tải bởi vì người viết và người đọc luôn có hệ quy chiếu và thế giới quan khác nhau, nên việc hiểu hết 100% ý tác giả (tức là nguyên xi) là không tưởng. Nhưng cũng đâu cần phải đạt được mức hoàn hảo đó, bởi chúng ta chỉ cần hiểu THÔNG ĐIỆP của sách và quan trọng là áp dụng vào cuộc sống và cách hiểu của mình thôi mà.
Vậy bí quyết ở đây là hãy lược bỏ con chữ đi để nắm bắt thông điệp được tốt hơn. Để mình lấy một ví dụ, khi mình học IELTS, mình thường phải đọc những bài viết mà mình không hề biết hết tất cả các từ trong đó, nhưng chỉ nhờ những câu mình biết, hoặc mình đoán ra nghĩa của nó; sau khi xâu chuỗi lại mình đã có thể hiểu được bài viết muốn nói về điều gì. Điều này chứng minh rằng không cần cứ phải đọc hết tất cả nội dung con chữ trong sách để thâu tóm được thông điệp của sách. Và để không cần phải đọc hết nội dung con chữ, bạn có một cách, đó là ĐỌC LƯỚT.
- ĐỌC LƯỚT ở những chỗ mô tả, đi sâu vào chi tiết. Ví dụ trong sách văn học hay sách khoa học, sách kinh tế, phát triển bản thân, sẽ có rất nhiều đoạn tác giả dẫn dắt bằng những câu chuyện, họ sẽ đi sâu vào miêu tả những chi tiết thừa thãi, việc của bạn là nhận ra những chỗ nào tác giả đang đi lệch ra khỏi nội dung họ muốn nói tới và bỏ qua nó.
- ĐỌC LƯỚT bằng cách xem mục lục để xem sách hệ thống nội dung như thế nào, để ta có thể có cái nhìn tổng quan hơn về sách. Trong mỗi chương lớn, xem trong đó những chương nhỏ đề cập tới vấn đề gì, vấn đề nào mình cần đọc, muốn đọc, vấn đề nào không cần đọc lại nữa (vì có thể đã thấm nhuần khi đọc sách hoặc tài liệu khác). Có nhiều sách mà tác giả đã rất tâm lý khi cuối mỗi chương có tổng kết lại các ý chính, bạn cũng có thể tận dụng nguồn này để hiểu nhanh hơn thông điệp sách muốn truyền tải.
- ĐỌC LƯỚT với một cây bút chì, sẵn sàng khoanh vào chỉ 3,4 câu trong một chương. Đừng khoanh quá nhiều ý trong một chương, càng khoanh ít chứng tỏ bạn càng biết nội dung chương đó đang xoay quanh vấn đề gì. Thường thì trong một chương sẽ có rất nhiều mô tả, ví dụ, dẫn dắt xoay quanh Ý CHÍNH của chương đó, vậy nên khi đọc hãy luôn tự hỏi Ý CHÍNH mà tác giả đang muốn đề cập tới ngay từ đầu là gì. Khi nào cảm thấy tác giả đang xa rời nó, sẵn sàng BỎ QUA không đọc tiếp. Tốt hơn nữa thì có một quyển sổ để ghi chép và tổng hợp lại những ý chính trong sách mà mình tìm được. Vẫn nguyên tắc CÀNG NGẮN GỌN CHỨNG TỎ CÀNG HIỂU SÁCH.
- ĐỌC LƯỚT bằng cách ĐỌC NHIỀU HƠN. Đọc nhiều hơn sẽ tự động sinh ra cho bạn TRỰC GIÁC biết rằng đoạn nào tác giả đang "lan man" và bạn sẽ dũng cảm và khôn ngoan hơn để bỏ qua đoạn đó. ĐỌC NHIỀU HƠN sẽ giúp bạn có được khối lượng kiến thức và sự thông hiểu tốt sẵn có về một vấn đề, để đến khi chạm vào vấn đề đó ở một cuốn sách khác, bạn không cần phải mất nhiều thời gian cho nó nữa. Hãy nhớ: RẤT NHIỀU SÁCH ĐỀ CẬP NHỮNG VẤN ĐỀ GIỐNG NHAU, CHỈ LÀ CÁCH DIỄN ĐẠT KHÁC NHAU MÀ THÔI.
4/ GẠT BỎ TÂM LÝ PHẢI THUỘC LÒNG NỘI DUNG SÁCH TRONG BẠN.
Khi đọc một cuốn tiểu thuyết văn học, hay sách phát triển bản thân, hay sách gì gì đó, chúng ta thường có tâm lý là muốn phải NHỚ được sách nói về cái gì. Nhưng chúng ta lại muốn từ NHỚ phải thật hoàn hảo bằng cách nhớ tất cả các nội dung, thông điệp sách muốn truyền tải. Xin thưa rằng đây là một ước muốn rất hoang đường.
Khi bạn đọc một quyển giáo trình (sách giáo khoa của sinh viên đó, nói thế cho mấy bạn trung học hiểu) thì bạn không bao giờ có tư tưởng phải nhớ tất cả những gì mình đọc được sau lần đọc đầu tiên, đúng không? Bạn phải đọc đi đọc lại nó, làm bài tập nhiều lần thì bạn mới nhớ, mà không phải bạn ép bản thân nhớ mà là bạn sẽ tự nhớ được. Thế mới hay.
Để nhớ được một cái gì đó, bạn có thể ép mình nhớ, nhưng cách này xem ra thường rất mệt và quên cũng rất nhanh (trong đa số các trường hợp); cách khác là bạn để nó tự nhiên nhớ, bằng cách gặp lại nó nhiều lần. Giống như bạn nghe tên 1 người lần đầu, bạn khó có thể nhớ ngay (chỉ là 1 cái tên thôi đấy), nhưng nếu được nghe người ta nhắc đi nhắc lại, hoặc chính bạn nhắc lại tên họ vài lần, bạn sẽ tự nhớ. Vậy thì làm sao chúng ta có thể ép mình phải nhớ nội dung của một cuốn sách chỉ sau 1 lần đọc được, đúng không? Không phải trí nhớ bạn kém, đơn giản là bởi tuyệt đại đa số đầu óc con người được thiết kế như vậy mà thôi.
Vậy thì muốn nhớ: thỉnh thoảng hãy lôi sách ra đọc lại những dòng mà các bạn đã đánh dấu, hoặc ghi chép lại trong sổ tay. Cuốn nào mà các bạn không cầm ra đọc lại, tức là nó cũng chẳng cần thiết để đọc lại với bạn lắm, nên không cần phải lăn tăn nhiều nhé.
5/ LUYỆN TẬP.
Thay vì nói ra một đống những cách thức đọc khác nhau hay viết ra ti tỉ những bước phải làm để đọc nhanh, mình chỉ mong các bạn thực hành được 2 điều này thôi là đã quá tốt rồi:
1. ĐỌC THEO CỤM TỪ:
Đúng vậy, thay vì đọc từng chữ từng chữ một, bạn hãy tập cho mắt các bạn mở rộng phạm vi ra hơn, hãy nhìn và đọc hiểu theo cả cụm. Lúc đầu là cụm 3 chữ, 4 chữ, dần dần các bạn sẽ đạt tới khả năng chia 1 câu ra thành 2,3 cụm là chuyện bình thường. Lúc đầu có thể khó khăn, nhưng chỉ cần bạn vượt qua được ngưỡng khó chịu đó thì bạn có thể làm được chỉ sau 1,2 quyển sách mà thôi. Cơ bản khó chịu là vì bạn chưa quen, chứ quen rồi thì cảm giác rất dễ chịu. Sẽ tốt hơn nếu bạn có một cây bút dẫn đường cho mắt, mắt sẽ tập trung và tốc độ đọc cũng sẽ nhanh hơn.
2. ĐỌC NHIỀU
Vẫn là đọc nhiều, càng đọc nhiều, bạn càng có môi trường để luyện tập, càng luyện tập nhiều, bạn càng giỏi. Vậy thôi.
6/ ĐỌC LÀ ĐỌC, SUY NGẪM LÀ SUY NGẪM.
Tác dụng của việc đọc nhanh, đọc lướt là để bạn có cái nhìn bao quát và hệ thống được sách đang nói về điều gì, sau đó bạn vẫn có thời gian để xem lại những chỗ mình đánh dấu và đánh giá xem mình có nên đọc lại hay không mà.
Nhiều người (và cả mình trước đây) cũng rất thích kiểu vừa đọc vừa ngẫm. Ok, không sao cả, vì nó rất là hay. Nhưng trong phạm vi về phương pháp đọc nhanh, mình sẽ không đề cập đến nó. Suy cho cùng, sau khi bạn đã có cái nhìn tổng quát và lọc ra được những ý chính mình cần chú trọng thì bạn vẫn có thời gian để suy ngẫm cơ mà. Hãy nhớ rằng:
Bạn có thể SUY NGẪM trong quá trình ĐỌC. Nhưng bạn KHÔNG THỂ ĐỌC trong quá trình SUY NGẪM.
Có thể bạn vừa đọc vừa suy nghĩ, nhưng như thế thời gian sẽ lâu hơn và có khả năng cao là bạn cũng sẽ mất thời gian để hoàn thành một cuốn sách hơn, có thể là còn chẳng bao giờ hoàn thành nó. Thay vì vậy, chọn một cách nhẹ nhàng hơn, ĐỌC XONG RỒI SUY NGẪM, chia nó ra làm 2 công đoạn, vậy chẳng phải nhẹ nhàng và sướng hơn sao?
-----------------------------------------------------------------------------
Phù, viết được xong cái bài này cũng bở cả hơi tai. Nhưng hi vọng rằng nó sẽ giúp ích được cho các bạn trong quá trình đọc sách.
Mình tin rằng khi các bạn hiểu được những điều đơn giản này thì không cần phải tự làm khổ mình với những cuốn sách dạy đọc nhanh nữa, bởi thực ra không phải ai cũng đủ kiên trì và nỗ lực để tập luyện chúng.
Như mình đã nói, đọc sách nhanh có lợi cho bạn rất nhiều, nhưng trước khi đọc nhanh, chúng ta phải hiểu bản chất chữ nhanh là gì, nhanh là như thế nào, và nhanh ở đâu. Chỉ có vậy thì chúng ta mới có thể đọc nhanh hơn được.
Hy vọng rằng bài viết sẽ mang lại những giá trị thiết thực cho các bạn, giúp các bạn bớt khổ hơn khi đọc. See you again! :)
P/s: Bài mình viết nhìn dài như thế nhưng cũng chỉ có một vài THÔNG ĐIỆP và KEYWORD (TỪ KHÓA) mà thôi. Nếu nắm được chúng, các bạn cứ comment cho mình biết nhé ^^
Ảnh tốt nghiệp Wollongong
https://www.flickr.com/photos/134852063@N08/albums: trang web về ảnh tốt nghiệp ở UOW
Khuyến học Fukuzawa Yukichi
https://www.youtube.com/watch?v=pXm9zD7dLeU: video youtube về sách Khuyến học.
http://khosachnoi.com.vn/sach-noi/810/khuyen-hoc.html
https://www.youtube.com/channel/UCKvdwwCjKH45dS_eHRkLhoQ/videos: đây cũng là trang web hay về sách nói, sách nói online
http://khosachnoi.com.vn/sach-noi/810/khuyen-hoc.html
https://www.youtube.com/channel/UCKvdwwCjKH45dS_eHRkLhoQ/videos: đây cũng là trang web hay về sách nói, sách nói online
Khuyến học Fukuzawa Yukichi
https://www.youtube.com/watch?v=pXm9zD7dLeU: video youtube về sách Khuyến học.
http://khosachnoi.com.vn/sach-noi/810/khuyen-hoc.html
https://www.youtube.com/channel/UCKvdwwCjKH45dS_eHRkLhoQ/videos: đây cũng là trang web hay về sách nói, sách nói online
http://khosachnoi.com.vn/sach-noi/810/khuyen-hoc.html
https://www.youtube.com/channel/UCKvdwwCjKH45dS_eHRkLhoQ/videos: đây cũng là trang web hay về sách nói, sách nói online
CÁC NHÀ KHOA HỌC VÀ NHỮNG PHÁT MINH - CHÌA KHÓA VÀNG TRI THỨC
http://www.emiclib.com/ViewAudio/2258/5360/3/443/0/: một trang sách nói khá hay
Thứ Tư, 22 tháng 6, 2016
Kho sách nói - Tư duy tích cực thay đổi cuộc sống
Đây là một cuốn sách hay, viết về các chân lý đơn giản trong cuộc sống. Chính vì sự đơn giản của các chân lý này mà nhiều người đã quên, làm ngơ và dẫn đến một cuộc sống bi quan.
Thứ Hai, 20 tháng 6, 2016
20 nhà toán học vĩ đại đã làm thay đổi thế giới
Source http://diendantoanhoc.net
Nhờ họ mà thế giới hiện đại mới có được sự phát triển và tiến bộ như ngày nay.
Trước khi các nhà khoa học có thể phát triển phương thuốc mới hay các kỹ sư có thể nâng cấp công nghệ, họ phải viết tất cả thông tin cũng như các con số lên tấm bảng trắng. Tất cả đều phải sử dụng những mô hình toán cao cấp – di sản của các nhà toán học vĩ đại để lại cho thế giới.
Có thể nhiều người không đồng quan điểm nhưng thực tế, không một lĩnh vực học thuật nào lại có vai trò lớn hơn toán học trong lịch sử nhân loại.
Tuy nhiên, các nhà toán học lại thường chỉ được ghi nhận và vinh danh khá khiêm tốn so với những gì họ đã đóng góp.
Dưới đây là 20 nhà toán học lỗi lạc với những đóng góp quan trọng, cấu thành nên thế giới hiện đại ngày nay
1. Wliiam Playfair – Người phát minh ra đồ thị

Ông là kỹ sư người Scotland, cha đẻ của “số liệu đồ họa” bao gồm có: đồ thị dạng thanh, dạng bánh, thậm chí cả timelines (dòng thời gian)
2. James Maxwell – Người tạo ra những bức ảnh màu đầu tiên

Nhà toán học người Scotland. Ông được Einstein ngưỡng mộ ngang với Micheal Faraday hay Newton.
3. Alan Turing – Người “mã hóa” trong thế chiến thứ 2

Nhà toán học người Anh. Ông cũng là người đặt nền móng cho chiếc PC phổ biến hiện nay.
4. Pierre-Simon Laplace – Người tiên phong trong môn thống kê

Người đã tiên đoán về sự tồn tại của hố đen vũ trụ, một trong những người đầu tiên nghiên cứu về vận tốc âm thanh
5. Thomas Bayes – Người phát triển môn thống kê

Người đặt nền móng cho môn thống kê Bayes. Định lý toán của ông đặc biệt hữu dụng trong lĩnh vực dự đoán thống kê
6. Charles Babbage – Người có tầm nhìn trong ngành máy tính

Nhà phát minh và nhà toán học người Anh, người được cho là “cha đẻ ngành máy tính”
7. Ada Lovelace – Nhà lập trình máy tính đầu tiên

Cộng tác cùng Charles Babbage, nữ bá tước Ada Lovelace cũng được tôn xưng là nhà lập trình máy tính đầu tiên trong lịch sử
8. David Hilbert – Người cổ vũ nền toán học

Năm 1900, ông đã gây tiếng vang khi tập hợp đủ 23 vấn đề chưa được giải quyết trong toán, những công trình có thể dẫn tới những tiến bộ trong thế kỷ 20. Nhờ hành động này, Hilbert đã khích động và thôi thúc cả một thế hệ các nhà toán học
9. Euclid of Alexandria – Nhà khai sáng

Nhà toán học cổ đại người Hy Lạp, một trong những người đầu tiên hệ thống hóa toàn bộ các kiến thức về toán
10. Issac Newton – Người phát minh môn giải tích

Nhà toán học, vật lý lỗi lạc với các giả thuyết về trọng lực cũng như môn tích phân
11. Gottfried Leibniz – Dưới cái bóng của Newton
Tuy không nổi tiếng như Newton nhưng Leibniz cũng là người phát minh môn giải tích độc lập với Newton. Ông cũng là người phát triển nhiều ứng dụng dựa trên bảng tính Pascan
12. Joseph Lagrange – Đơn giản hóa công việc của Newton
Ông đã tái công thức hóa và đơn giản lại các hàm toán học của Newton. Lagrange được chon cất tại Pantheon, lăng mộ quốc gia dành cho những người Pháp vĩ đại.
13. Blaise Pascal – Người phát minh chiếc máy tính đầu tiên
Ông có rất nhiều đóng góp cho nhân loại, bao gồm việc sử dụng sức nước, sáng tạo ra hệ thống vòi phun cũng như chiếc máy tính cơ học đầu tiên.
14. John von Neumann – Nhà phát triển máy tính kỹ thuật số
Ông là người lai Hungari – Mỹ. Ngoài những cống hiến cho ngành máy tính, ông cũng là người nghiên cứu về các loại phản ứng hạt nhân.
15. Leonhard Euler – Nhà toán học và trí tưởng tượng phong phú
Nhà toán học người Thụy Sĩ, người có nhiều đề xuất quan trọng như chữ cái “e” cho logarit cơ số tự nhiên, “I” biểu diễn số ảo và biểu tượng sigma với ý nghĩa tổng hợp.
16. Daniel Bernoulli – Xây dựng nền móng của ngành khí động lực học
Ông cũng là một người Thụy Sĩ, ngoài ra ông cũng là nhà tiên phong trong lĩnh vực dược phẩm
17. Carl Freidrich Gauss – Người đứng sau môn thống kê
Nhà toán học người Đức và được coi là một trong những nhà toán học có ảnh hưởng nhất lịch sử
18. Joseph Fourier – Người giải thích hiệu ứng nhà kính
Ông là người có những đóng góp quan trọng trong môn nhiệt động lực học, cũng như giải thích sự bức xạ nhiệt, sự tác động của bầu khí quyển tới việc duy trì nhiệt độ.
19. Theodore von Kármán – Đóng góp quan trọng để phát triển máy bay trực thăng và máy bay siêu âm
Sinh trưởng tại Budapest – thủ đô Hungary, ông là người tạo dựng công ty Aerojet. Ông cũng chính là người tạo dựng trung tâm nghiên cứu hàng không của Nato
20. Stanislaw Ulam – Nhà phát triểm mô hình mô phỏng Monte Carlo
Người có đóng góp vô cùng quan trọng trong ngành vật lý hạt nhân. Phương pháp mô phỏng Monte Carlo của ông đang được ứng dụng rất rộng rãi trên thế giới ngày nay.
Theo TTVN/BI
- funcalys, L Lawliet, Mai Duc Khai và 3 người khác yêu thích
#2  Khanh 6c Hoang Liet
Khanh 6c Hoang Liet
Đã gửi 11-11-2012 - 16:26
Pythagoras

Ông nổi tiếng với định lý Pythagore trong lượng giác. Tuy nhiên, một số người nghi ngờ liệu ông có phải là người đã đưa ra các chứng minh hay không vì họ cho rằng người đã đưa ra các chứng mình là học trò của ông có tên là Baudhayana, sống tại Ấn Độ khoảng 300 năm về trước.
Thực sự, Định lý Pythagore là một phát minh có vai trò quan trọng đối với sự phát triển của hình học, mở ra những nghiên cứu sâu và có ý nghĩa to lớn. Chính vì vậy Pythagore được công nhận là cha đẻ của Toán học hiện đại.
Andrew Wiles

Andrew Wiles, nhà toán học duy nhất còn sống trong danh sách này, là một người nổi tiếng với chứng minh Định lý cuối cùng của Fermat: "Không tồn tại các nghiệm nguyên khác không a, b, và c thoả an + bn = cn trong đó n là một số nguyên lớn hơn 2."
Sau gần 8 năm nghiên cứu. Mặc dù những đóng góp của Andrew Wiles chưa thể sánh với những cái tên trong danh sách ở đây, nhưng ông là người đã "phát minh" ra phần lớn toán học mới để chứng minh các định lý.
Ngoài ra, ông cũng là một trong những người có cống hiến đáng ngưỡng mộ, như đã tự giam mình trong 7 năm để nghiên cứu giải pháp toán học. Khi nhận thấy lỗi trong các giải pháp, ông lại một mình tìm ra giải pháp hoàn chỉnh trong một năm trước khi chúng được thế giới chấp nhận.
Isaac Newton và Wilhelm Leibniz

Đây là hai nhà khoa học được vinh dự trở thành người sáng tạo ra toán học vi phân. Leibniz đã phát minh ra vi phân độc lập Isaaw Newton, với những kí hiệu được sử dụng phổ biến. Bên cạnh đó Leibiniz đã khám phá ra hệ thống số nhị phân, tạo nền tảng phát triển máy tính hiện đại.
Trong khi đó, nhà thiên tài Isaac Newton, cũng để lại cho nhân loại một gia tài tri thức vĩ đại. Cùng với Leibiniz, Newton đã phát triển phép tính vi phân và tích phân.
Leonardo Pisano Blgollo

Blgollo (1170-1250), còn được biết đến với tên gọi là Leonardo Fibonacci, được coi là một trong những nhà toán học vĩ đại nhất thời trung cổ. Người ta vẫn ca ngợi ông là một nhà toán học Ấn Độ lừng lẫy từ khoảng 200 năm trước Công nguyên, và còn đóng góp rất nhiều cho sự ra đời của hệ thống đánh số Ả Rập. Với những đóng góp của mình ông đã được công nhận là ngươi có vai trò quan trọng trong sự phát triển toán học hiện đại.
Alan Turing

Sau khi kết thúc chiến tranh, ông dành thời gian của mình để nghiên cứu máy tính, và trở thành nhà khoa học máy tính thực sự đầu tiên của thế giới. Ông có rất nhiều tài liệu quan trọng vẫn còn áp dụng trong thời đại mới.
Ông đã đưa ra công thức cho khái niệm thuật toán và tính toán với máy Turing (một mô hình về thiết bị xử lý các ký tự, đơn giản, nhưng có thể thực hiện được tất cả các thuật toán máy tính), đồng thời đưa ra phiên bản của "Turing" được sử dụng cho tới ngày nay.René Descartes

René Descartes đã có những đóng góp đột phá đối với Toán học. Cùng với Newton và Leibniz, René Descartes đã cùng sáng tạo ra nền tảng cho phép tính hiện đại, mang rất nhiều ý nghĩa to lớn đối với đời sống con người ngày nay.
Đóng góp quan trọng nhất của René Descartes đối với lĩnh vực Toán học có lẽ là những đóng góp trong lĩnh vực hình học giải tích. Tên của ông được đặt cho hệ trục tọa độ vuông góc (Trục tọa độ Đề-các vuông góc). Bên cạnh đó ông còn góp phần vào sự phát triển của các kí hiệu toán học hiện đại.
Euclid

Thật không may, chẳng mấy ai biết đến sự tồn tại của ông cũng như sự nghiệp của ông cho tới sau khi ông qua đời. Với những ai chưa từng biết đến ông, thì đây là cơ hội để nói lời cám ơn đối với sự cống hiến khai phá kiến thức nhân loại tuyệt vời của Euclid.
G. F. Bernhard Riemann

G. F. Bernhard Riemann, sinh ra trong một gia đình nghèo vào năm 1826, và được nuôi dưỡng trở thành một trong những nhà toán học nổi tiếng thế giới của thế kỷ 19. Tên của ông nằm trong danh sách những người có những đóng góp to lớn cho Hình học, phải kể đến là Hình học Riemann, mặt Riemann và tích phân Riemann. Nhưng có lẽ điều làm cho ông trở nên nổi tiếng nhất (hoặc là “tai tiếng”) đó là Giả thuyết Riemann - nói về vấn đề phân bố của các số nguyên tố - làm đau đầu nhân loại suốt hơn 150 năm qua. Ông đã giới thiệu hàm số Riemann zeta và áp dụng để hiểu được sự phân bố của số nguyên tố.
Carl Friedrich Gauss

Thần đồng Gauss được người đời gọi là “Hoàng tử Toán học” đã có những khám phá đầu tiên khi mới chỉ là một cậu thiếu niên. Nhiều người đã thực sự ngỡ ngàng trước cậu bé Gauss tuổi với khả năng tính tổng 100 số chỉ trong… vài giây.
Gauss có nhiều đóng góp rất quan trọng cho toán học đại số và lý thuyết số. Ngoài ra ông còn đưa ra hằng số Gauss, nghiên cứu về hiện tượng từ tính, và tên của ông đã được đặt cho đơn vị từ trường. Tất cả những điều này được thực hiện trước sinh nhật lần thứ 24 của ông. Và cho đến cuối đời, ông vẫn miệt mài nghiên cứu và cống hiến cho nhân loại. Ông qua đời ở tuổi 77.
Leonhard Euler

Nếu Gauss được gọi là “Hoàng tử” thì Euler xứng đáng được gọi là “Vị vua của toán học”. Euler sinh năm 1707 và mất năm 1783, được công nhận là nhà toán học vĩ đại nhất hành tinh.
Người ta kể rằng tất cả các công thức toán học được đặt theo tên của những người còn đứng sau cả Euler. Trong thời đại của mình, Euler đã có những đóng góp đột phá và được sánh ngang bằng với nhà bác học đại tài Einstein về trí tuệ.
Ông đã giới thiệu hệ thống các kí hiệu toán học kèm với các định nghĩa của công thức (chẳng hạn như f(x)), chữ viết tắt hàm lượng giác, chữ “e” là cơ sở của logarit tự nhiên (Hằng số Euler), chữ cái Hy Lạp Sigma biểu thị “Tổng kết”, biểu tượng Pi thể hiện tỉ lệ của chu vi hình tròn đối với đường kính của nó… Tất cả còn được áp dụng cho tới ngày nay.
Ông là người đã giải quyết vấn đề đặt ra trong bài toán “Bảy chiếc cầu ở Koenigsberg” nổi tiếng, tạo nền tảng liên kết số đỉnh, cạnh và bề mặt của đối tượng. Ông cũng là người đã chứng minh rất nhiều lý thuyết nổi tiếng của thế giới.
Hơn thế nữa, ông còn phát triển toán phép tính, cấu trúc liên kết, lý thuyết số, thuyết đồ thị và phân tích… mở đường cho toán học hiện đại và những bước tiến sau này của nó. Giờ thì chúng ta biết rằng, không phải ngẫu nhiên mà công nghiệp và công nghệ đương thời lại phát triển nhanh như vũ bão.
- Nguyen Minh Tuan B, tramyvodoi và PolarBear154 thích
Chủ Nhật, 19 tháng 6, 2016
How Polynomials Behave
Source http://www.mathsisfun.com/algebra/polynomials-behave.html
A polynomial looks like this:
The graph is symmetrical about the y-axis, which means the function is even. This rules out answer A.
The graph is upside down indicating that the power of x should be preceded by a negative. This means the answer could be B or D.
Since the curve is flattened at the top and does not show the characteristic shape of a parabola, we conclude that B is the correct answer.
Furthermore, the y-intercept is 3 which agrees with this answer.
![[image]](https://www.mathopolis.com/questions/images/4/c/dd94d138b44fb0a5610fed6f3e05272.jpg)
The above shows the graph of y = 2x5- 6x3
How many turning points does it have?
A polynomial looks like this:
 | ||||||||||||||||||||||||
example of a polynomialContinuous and Smooth
There are two main things about the graphs of Polynomials:
The graphs of polynomials are continuous, which is a special term with an exact definition in calculus, but here we will use this simplified definition:
 we can draw it without lifting our pen from the paper we can draw it without lifting our pen from the paper
The graphs of polynomials are also smooth. No sharp "corners" or "cusps"
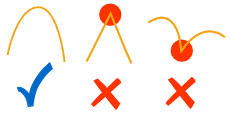 How the Curves Behave
Let us graph some polynomials to see what happens ...
... and let us start with the simplest form:
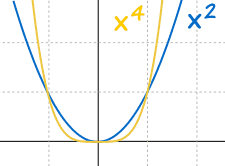
f(x) = xn
Which actually does interesting things:
And:
Power Function of Degree n
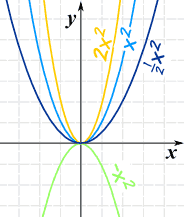
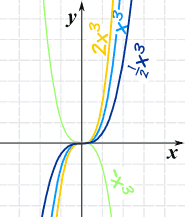
Next, by including a multiplier of a we get what is called a "Power Function":
f(x) = axn
f(x) equals a times x to the "power" (ie exponent) n
The "a" changes it this way:
We can use that knowledge when sketching some polynomials:
Example: Make a Sketch of y=1−2x7
Start with the simplest "odd power" graph of x3, and gradually turn it into 1−2x7
Like this:
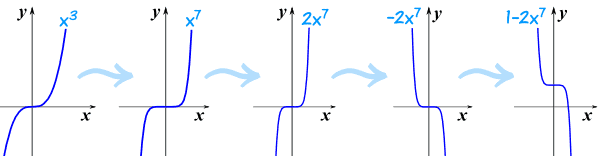
So by doing this step-by-step we can get a good result.
Turning Points
A Turning Point is an x-value where a local maximum or local minimum happens:
 How many turning points does a polynomial have?
Never more than the Degree minus 1
The Degree of a Polynomial with one variable is the largest exponent of that variable.
 Example: a polynomial of Degree 4 will have 3 turning points or less
The most is 3, but there can be less.
We may not know where they are, but at least we know the most there can be!
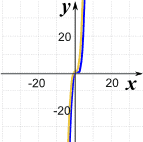
What Happens at the Ends
And when we move far from zero:
then the graph starts to resemble the graph of y = axn where axn is the term with the highest degree.
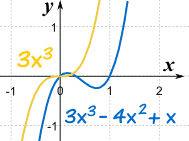
Example: f(x) = 3x3−4x2+x
Far to the left or right, the graph will look like 3x3
This makes sense, because when x is large, then x3 is much greater than x2 etc
This is officially called the "End Behavior Model".
And yes, we have come to the end!
Summary
![[image]](https://www.mathopolis.com/questions/images/0/e/8e951727655dca3864ffb2d46b9b642.jpg) Which one of the following could be the function for the above graph?
A
f(x) = 3 - 2x5
B
f(x) = 3 - 2x6
C
f(x) = 3 + 2x6
D
f(x) = 3 - 2x2
|
The graph is upside down indicating that the power of x should be preceded by a negative. This means the answer could be B or D.
Since the curve is flattened at the top and does not show the characteristic shape of a parabola, we conclude that B is the correct answer.
Furthermore, the y-intercept is 3 which agrees with this answer.
![[image]](https://www.mathopolis.com/questions/images/4/c/dd94d138b44fb0a5610fed6f3e05272.jpg)
The above shows the graph of y = 2x5- 6x3
How many turning points does it have?
A
2
B
3
C
4
D
Cannot say
+0.50
Excellent ... you are right.
At a maximum turning point the slope of the curve changes from positive to zero to
negative - there is a maximum turning point at approximately (-1.4, 5.8).
At a minimum turning point the slope of the curve changes from negative to zero to
At a minimum turning point the slope of the curve changes from negative to zero to
positive - there is a minimum turning point at approximately (1.4, -5.8).
At the origin the slope of the curve changes from negative to zero and then back to
At the origin the slope of the curve changes from negative to zero and then back to
negative - this is called a point of inflection and is not a turning point.
Far away from the origin the graph of y = 2x5-6x3 behaves like the graph of y = 2x5,
Far away from the origin the graph of y = 2x5-6x3 behaves like the graph of y = 2x5,
so there will be no further turning points.
Therefore, there are just 2 turning points.
![[image]](https://www.mathopolis.com/questions/images/d/7/76fa4091499c3bf03eb7eede8489e12.jpg)
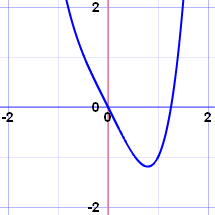
Which one of the following could be the function for the above graph?
Therefore, there are just 2 turning points.
![[image]](https://www.mathopolis.com/questions/images/d/7/76fa4091499c3bf03eb7eede8489e12.jpg)
Which one of the following could be the function for the above graph?
A
f(x) = 1 - 3x4
B
f(x) = 1 + 3x4
C
f(x) = (1 - 3x)4
D
f(x) = (1 + 3x)4
+0.50
Excellent ... you are right.
The graph is symmetrical about the y-axis, which means the function is even.
When expanded the answers C and D have both even and odd powers, so they are
neither even nor odd functions. So the answer cannot be C or D.
Which leaves only A or B.
The graph is upside down indicating that the power of x should be preceded by a negative.
Therefore the answer is A.
![[image]](https://www.mathopolis.com/questions/images/d/5/994f6c1e94c06ab48cdf26a22abcbd2.jpg)
Which one of the following could be the function for the above graph?
correct answer
![[image]](https://www.mathopolis.com/questions/images/2/2/562e63ef48954674c409a9e547ee412.gif)
Using the Function Grapher, my first attempt to the solution is that it has a minimum point somewhere between x = -1 and x = 0.
![[image]](https://www.mathopolis.com/questions/images/e/f/e8499e4672751fe7a4518c09b0a8f02.gif)
When I zoom in, I get a better approximation, which is the point (-0.6, -0.9) to 1 decimal place.
So the minimum value of the function is -0.9 correct to 1 decimal place.
(Note: the function could have been simplified to f(x) = 2x4 + 2x)
When expanded the answers C and D have both even and odd powers, so they are
neither even nor odd functions. So the answer cannot be C or D.
Which leaves only A or B.
The graph is upside down indicating that the power of x should be preceded by a negative.
Therefore the answer is A.
![[image]](https://www.mathopolis.com/questions/images/d/5/994f6c1e94c06ab48cdf26a22abcbd2.jpg)
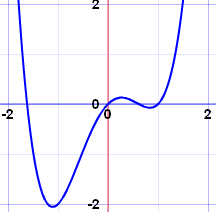
Which one of the following could be the function for the above graph?
A
y = x6 - 5x4 + 7x2
B
y = x3 + 7x
C
y = x5 - 5x3 + 7x
D
y = x5 - 5x2 + 7x
+0.50
Yes! Well Done.
The graph has point symmetry about the origin, which means the function is odd.
This rules out answer A which is even and answer D, which is neither even nor odd.
The graph has 4 turning points, so it cannot be a cubic - a cubic has at most 3 - 1 = 2
The graph has 4 turning points, so it cannot be a cubic - a cubic has at most 3 - 1 = 2
turning points. So answer B cannot be correct.
A quintic, on the other hand, has at most 5 - 1 = 4 turning points, so C could be the
A quintic, on the other hand, has at most 5 - 1 = 4 turning points, so C could be the
correct answer
Use the Function Grapher at http://www.mathsisfun.com/data/function-grapher.php to find an estimate, correct to 1 decimal place, of the minimum value of the function
f(x) = 5x4 - 3x4 + 2x
(Note: enter function as 5x^4-3x^4+2x ... or in a simpler form if you can think how.)
f(x) = 5x4 - 3x4 + 2x
(Note: enter function as 5x^4-3x^4+2x ... or in a simpler form if you can think how.)
A
-0.6
B
-0.8
C
-0.9
D
-1.9
+0.50
Congratulations, that is the right answer.
![[image]](https://www.mathopolis.com/questions/images/2/2/562e63ef48954674c409a9e547ee412.gif)
Using the Function Grapher, my first attempt to the solution is that it has a minimum point somewhere between x = -1 and x = 0.
![[image]](https://www.mathopolis.com/questions/images/e/f/e8499e4672751fe7a4518c09b0a8f02.gif)
When I zoom in, I get a better approximation, which is the point (-0.6, -0.9) to 1 decimal place.
So the minimum value of the function is -0.9 correct to 1 decimal place.
(Note: the function could have been simplified to f(x) = 2x4 + 2x)
Đăng ký:
Nhận xét (Atom)
Tìm kiếm Blog này
Nhãn
- Thú vị (40)
- Tài liệu giảng dạy (39)
- Tài liệu tham khảo (20)
- Coursera courses (17)
- Ứng dụng toán học trong cuộc sống (17)
- Giải trí (16)
- Toán tài chính (14)
- research skills (12)
- Đọc sách (12)
- Tin tức (9)
- Tiếng anh (7)
- Calculus (5)
- Kĩ năng tin học (5)
- Web hay (5)
- XSTK (3)
- Study skills (2)
- Toán cấp 3 (2)
- Matlab (1)
- Săn học bổng (1)
- Sống tâm huyết (1)
Lưu trữ Blog
-
▼
2016
(147)
-
▼
tháng 6
(61)
- Nguyễn Thanh Tùng | Ghi chép của một nhà khoa học trẻ
- LÀM THẾ NÀO ĐỂ TĂNG TỐC ĐỘ ĐỌC SÁCH MÀ KHÔNG CẦN H...
- Ảnh tốt nghiệp Wollongong
- Khuyến học Fukuzawa Yukichi
- Khuyến học Fukuzawa Yukichi
- CÁC NHÀ KHOA HỌC VÀ NHỮNG PHÁT MINH - CHÌA KHÓA VÀ...
- hocthenao.vn/
- Kho sách nói - Tư duy tích cực thay đổi cuộc sống
- MỘT KHO SÁCH TOÁN HAY - KHÁ ĐẦY ĐỦ
- 20 nhà toán học vĩ đại đã làm thay đổi thế giới
- Tai lieu cho Calculus
- Blog hay ve ung dung toan
- Interesting websites for maths
- Công cụ vẽ hình online
- How Polynomials Behave
- Intermediate Value Theorem
- Singapore maths
- Bài Ca Tình Yêu -Đinh Mạnh Ninh
- Dòng thời gian-Nguyễn Hải Phong
- Top 10 cuốn sách có thể thay đổi cuộc đời bạn
- GotIt-Vietnamese study experts
- Go Latex
- Facebook ghi lại ứng dụng toán
- Bí quyết đối nhân xử thế
- Markov chain approximations for Lévy processes 1: ...
- Markov Chains | Statistics 110
- Levy Processes and Applications to Machine Learning
- Brownian motion and Ito integral
- Fractional Calculus
- Quants Hub
- Hidden Markov Model
- MATLAB for Begineers for Quant Finance / Financial...
- Good websites
- Nucleus Medical Media
- Sách toán hay
- Probabilistic Systems Analysis and Applied Probabi...
- Tony Buổi Sáng (Audio Book)
- English Sharing-các bạn trẻ tâm huyết, tài năng
- Model Thinking by University of Michigan
- Welcome to Calculus One Jim Fowler, P6
- Welcome to Calculus One Jim Fowler, P5
- Welcome to Calculus One Jim Fowler, P4
- Welcome to Calculus One Jim Fowler, P3
- Applications of Linear Algebra (Part 1)
- MAT150x Math in Sports
- Welcome to Calculus One Jim Fowler, P2
- Welcome to Calculus One Jim Fowler, PhD
- Introduction to Regression
- Quantitative Methods by University of Amsterdam C 2
- PhD life
- Truyện cười
- Quantitative Methods by University of Amsterdam
- Nhập môn Khoa học máy tính
- Quy hoạch tuyến tính
- Fundamentals of Quantitative Modeling-Chapter 3
- Các trang web hay
- Fundamentals of Quantitative Modeling-Chapter 2
- PhD students
- Bóng đá
- Hỗ trợ công bố khoa học
- Từ chối làm bác sỹ ở Úc để về quê nhà khám bệnh ch...
-
▼
tháng 6
(61)